独力

• 个人简介

  独力，男，副教授，博士，硕士生导师。现为重庆理工大学理学院教师，美国数学会《数学评论》评论员。2016年6月毕业于西北师范大学，获理学博士学位。研究方向为子流形与几何分析，目前主要从事多调和映照，高能量泛函理论的相关研究工作，现已在已在国内外重要学术期刊 《Ann. Mat. Pura Appl. (1923-)》、《J. Geom. Phys.》、《J. Math. Anal. Appl.》、《Diff. Geom.Appl.》、《Math. Phys. Anal. Geom.》，《Mediterr. J. Math.》、《Math. Slovaca》和《数学年刊》等发表论文数篇。主持完成省部项目2项。先主持重庆市自然科学基金面上项目1项，现参与国家自然科学面上项目1项，省部级以上项目4项。担任《高等数学》，《线性代数》等全校公共课的教学任务。2020，2022和2023年度校级优秀教师。

• 研究领域

微分几何

• 承担的主要项目

  [1] 伪黎曼空间型中三调和子流形的研究，重庆市自然科学基金项目，2024.7-2027.6，10万，结题（主持）。

  [2] 体积泛函和Willmore泛函的几何变分问题, 国家自然科学基金项目，2023.1-2026.12， 47万，参与。

  [3] 解析函数空间算子理论的复向量丛方法，重庆市教委重点项目，2023.7-2026.7,12万，参与。

  [4] 基于机器学习的信用风险评价方法研究，重庆市自然科学基金项目，2021.10-2025.9，10万，参与。

  [5] 泊松几何中的胀开与形变量子化问题，重庆市教委科学技术研究项目，2022.10-2025.9，4万，参与。

  [6] 伪黎曼空间型中η-2-调和子流形的研究，重庆市自然科学基金项目，2019.7-2022.7，10万，结题（主持）。

  [7] 一般伪黎曼流形中双调和子流形的研究，重庆市教委科学技术研究项目，2019.10-2022.10，4万，结题（主持）。

  [8] Willmore泛函的若干问题研究，重庆市自然科学基金项目，2022.8-2024.8， 10万，结题（参与）。

• 代表性成果

[1] Du Li, Luo Yong, On minimality and scalar curvature of CMC triharmonic hypersurfaces in pseudo-Riemannian space forms, Ann. Mat. Pura Appl. (1923-) 2024, 203: 1793–1808.

[2] Du Li, Triharmonic hypersurfaces with constant mean curvature in pseudo-Riemannian space forms, J. Geom. Phys. 2023, 190: 104859.

[3] Du Li, On η-biharmonic hypersurfaces with constant scalar curvature in higher dimensional pseudo-Riemannian space forms, J. Math. Anal. Appl. 2023，518, 122670.

[4] Du Li, Ren Jinjun, On η-biharmonic hypersurfaces in pseudo-Riemannian space forms, Math. Slovaca. 2022,72: 1259-1272.

[5] Du Li, Zhang Juan, Biharmonic submanifolds with parallel normalized mean curvature vector field in pseudo-Riemannian space forms, Bull. Malays. Math. Sci. Soc. 2019, 42: 1469–1484.

[6] 独力，刘建成，Lorentz 空间型中2-调和超曲面的分类, 数学年刊, 2018, 39: 63-76.

[7] Du Li, Classification of 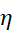-biharmonic surfaces in non-flat Lorentz space forms, Mediterr. J. Math., 2018, 15: 203.

[8] Du Li, Zhang Juan, Xie Xun, Hypersurfaces satisfying 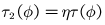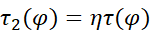in pseudo-Riemannian space forms, Math. Phys. Anal. Geom., 2017, 20: 17.

[9] Liu Jiancheng, Du Li, Minimality on biharmonic spacelike submanifolds in pseudo-Riemannian space forms, J. Geom. Phys., 2015, 92: 69-77.

[10] Liu Jiancheng, Du Li, Classification of proper biharmonic hypersurfaces in pseudo-Riemannian space forms, Diff. Geom.Appl., 2015, 41: 110-122.

• 联系方式

  E-mail：duli820210@cqut.edu.cn